Calculate I-squared values and variance distribution for multilevel meta-analysis models

This function calculates values of \(I^2\) and the variance distribution for multilevel meta-analysis models fitted with rma.mv.

Usage

mlm.variance.distribution(x)

Arguments

x

An object of class rma.mv. Must be a multilevel model with two random effects (three-level meta-analysis model).

Value

Returns a data frame containing the results. A plot summarizing the variance distribution and \(I^2\) values can be generated using plot.

Details

This function estimates the distribution of variance in a three-level meta-analysis model (fitted with the rma.mv function). The share of variance attributable to sampling error, within and between-cluster heterogeneity is calculated, and an estimate of \(I^2\) (total and for Level 2 and Level 3) is provided. The function uses the formula by Cheung (2014) to estimate the variance proportions attributable to each model component and to derive the \(I^2\) estimates.

References

Harrer, M., Cuijpers, P., Furukawa, T.A, & Ebert, D. D. (2019). Doing Meta-Analysis in R: A Hands-on Guide. DOI: 10.5281/zenodo.2551803. Chapter 12.

Cheung, M. W. L. (2014). Modeling dependent effect sizes with three-level meta-analyses: a structural equation modeling approach. Psychological Methods, 19(2), 211.

Author

Mathias Harrer & David Daniel Ebert

Examples

# Use dat.konstantopoulos2011 from the "metafor" package
library(metafor)
#> Loading required package: Matrix
#> Loading required package: numDeriv
#> 
#> Loading the 'metafor' package (version 4.2-0). For an
#> introduction to the package please type: help(metafor)

# Build Multilevel Model (Three Levels)
m = rma.mv(yi, vi, random = ~ 1 | district/school, data=dat.konstantopoulos2011)

# Calculate Variance Distribution
mlm.variance.distribution(m)
#>         % of total variance    I2
#> Level 1            4.812686   ---
#> Level 2           31.862476 31.86
#> Level 3           63.324838 63.32
#> Total I2: 95.19% 

# Use alias 'var.comp' and 'Chernobyl' data set
data("Chernobyl")
m2 = rma.mv(yi = z, V = var.z, data = Chernobyl, random = ~ 1 | author/es.id)
res = var.comp(m2)

# Print results
res
#>         % of total variance    I2
#> Level 1            1.254966   ---
#> Level 2           39.525499 39.53
#> Level 3           59.219534 59.22
#> Total I2: 98.75% 

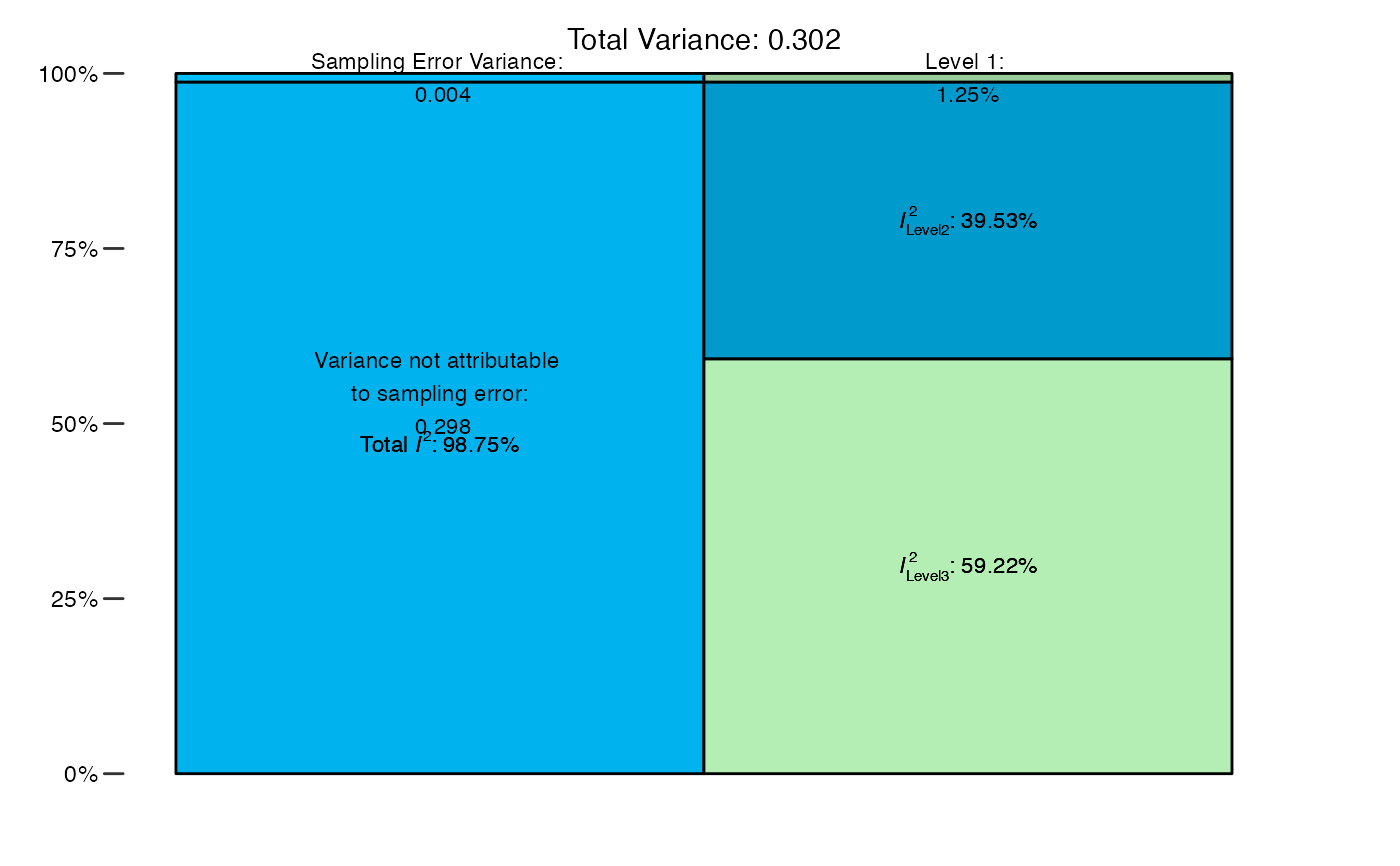
# Generate plot
plot(res)