Skip to contents

Perform a p-curve analysis

pcurve.Rd

This function performs a p-curve analysis using a meta object or calculated effect size data.

Usage

pcurve(x, effect.estimation = FALSE, N, dmin = 0, dmax = 1)

Arguments

x

Either an object of class meta, generated by the metagen, metacont, metacor, metainc, or metabin function, or a dataframe containing the calculated effect size (named TE, log-transformed if based on a ratio), standard error (named seTE) and study label (named studlab) for each study.

effect.estimation

Logical. Should the true effect size underlying the p-curve be estimated? If set to TRUE, a vector containing the total sample size for each study must be provided for N. FALSE by default.

N

A numeric vector of same length as the number of effect sizes included in x specifying the total sample size N corresponding to each effect. Only needed if effect.estimation = TRUE.

dmin

If effect.estimation = TRUE: lower limit for the effect size (d) space in which the true effect size should be searched. Must be greater or equal to 0. Default is 0.

dmax

If effect.estimation = TRUE: upper limit for the effect size (d) space in which the true effect size should be searched. Must be greater than 0. Default is 1.

Value

Returns a plot and main results of the pcurve analysis:

  • P-curve plot: A plot displaying the observed p-curve and significance results for the right-skewness and flatness test.

  • Number of studies: The number of studies provided for the analysis, the number of significant p-values included in the analysis, and the number of studies with p<0.025 used for the half-curve tests.

  • Test results: The results for the right-skewness and flatness test, including the pbinomial value, as well as the z and p value for the full and half-curve test.

  • Power Estimate: The power estimate and 95% confidence interval.

  • Evidential value: Two lines displaying if evidential value is present and/or absent/inadequate based on the results (using the guidelines by Simonsohn et al., 2015, see Details).

  • True effect estimate: If effect.estimation is set to TRUE, the estimated true effect ˆd is returned additionally.

If results are saved to a variable, a list of class pcurve containing the following objects is returned:

  • pcurveResults: A data frame containing the results for the right-skewness and flatness test, including the pbinomial value, as well as the z and p value for the full and half-curve test.

  • Power: The power estimate and 95% confidence interval.

  • PlotData: A data frame with the data used in the p-curve plot.

  • Input: A data frame containing the provided effect sizes, calculated p-values and individual results for each included (significant) effect.

  • EvidencePresent, EvidenceAbsent, kInput, kAnalyzed, kp0.25: Further results of the p-curve analysis, including the presence/absence of evidence interpretation, and number of provided/significant/p<0.025 studies.

  • I2: I2-Heterogeneity of the studies provided as input (only when x is of class meta).

  • class.meta.object: class of the original object provided in x.

Details

P-curve Analysis

P-curve analysis (Simonsohn, Simmons & Nelson, 2014, 2015) has been proposed as a method to detect p-hacking and publication bias in meta-analyses.

P-Curve assumes that publication bias is not only generated because researchers do not publish non-significant results, but also because analysts “play” around with their data ("p-hacking"; e.g., selectively removing outliers, choosing different outcomes, controlling for different variables) until a non-significant finding becomes significant (i.e., p<0.05).

The method assumes that for a specific research question, p-values smaller 0.05 of included studies should follow a right-skewed distribution if a true effect exists, even when the power in single studies was (relatively) low. Conversely, a left-skewed p-value distribution indicates the presence of p-hacking and absence of a true underlying effect. To control for "ambitious" p-hacking, P-curve also incorporates a "half-curve" test (Simonsohn, Simmons & Nelson, 2014, 2015).

Simonsohn et al. (2014) stress that p-curve analysis should only be used for test statistics which were actually of interest in the context of the included study, and that a detailed table documenting the reported results used in for the p-curve analysis should be created before communicating results (link).

Implementation in the function

To generate the p-curve and conduct the analysis, this function reuses parts of the R code underlying the P-curve App 4.052 (Simonsohn, 2017). The effect sizes included in the meta object or data.frame provided for x are transformed into z-values internally, which are then used to calculate p-values and conduct the Stouffer and Binomial test used for the p-curve analysis. Interpretations of the function concerning the presence or absence/inadequateness of evidential value are made according to the guidelines described by Simonsohn, Simmons and Nelson (2015):

  • Evidential value present: The right-skewness test is significant for the half curve with p<0.05 or the p-value of the right-skewness test is <0.1 for both the half and full curve.

  • Evidential value absent or inadequate: The flatness test is p<0.05 for the full curve or the flatness test for the half curve and the binomial test are p<0.1.

For effect size estimation, the pcurve function implements parts of the loss function presented in Simonsohn, Simmons and Nelson (2014b). The function generates a loss function for candidate effect sizes ˆd, using D-values in a Kolmogorov-Smirnov test as the metric of fit, and the value of ˆd which minimizes D as the estimated true effect.

It is of note that a lack of robustness of p-curve analysis results has been noted for meta-analyses with substantial heterogeneity (van Aert, Wicherts, & van Assen, 2016). Following van Aert et al., adjusted effect size estimates should only be reported and interpreted for analyses with I2 values below 50 percent. A warning message is therefore printed by the pcurve function when x is of class meta and the between-study heterogeneity of the meta-analysis is substantial (i.e., I2 greater than 50 percent).

References

Harrer, M., Cuijpers, P., Furukawa, T.A, & Ebert, D. D. (2019). Doing Meta-Analysis in R: A Hands-on Guide. DOI: 10.5281/zenodo.2551803. Chapter 9.2.

Simonsohn, U., Nelson, L. D., & Simmons, J. P. (2014a). P-curve: a Key to the File-drawer. Journal of Experimental Psychology, 143(2), 534.

Simonsohn, U., Nelson, L. D. & Simmons, J. P. (2014b). P-Curve and Effect Size: Correcting for Publication Bias Using Only Significant Results. Perspectives on Psychological Science 9(6), 666–81.

Simonsohn, U., Nelson, L. D. & Simmons, J. P. (2015). Better P-Curves: Making P-Curve Analysis More Robust to Errors, Fraud, and Ambitious P-Hacking, a Reply to Ulrich and Miller (2015). Journal of Experimental Psychology, 144(6), 1146-1152.

Simonsohn, U. (2017). R code for the P-Curve App 4.052. http://p-curve.com/app4/pcurve_app4.052.r (Accessed 2019-08-16).

Van Aert, R. C., Wicherts, J. M., & van Assen, M. A. (2016). Conducting meta-analyses based on p values: Reservations and recommendations for applying p-uniform and p-curve. Perspectives on Psychological Science, 11(5), 713-729.

See also

eggers.test

Author

Mathias Harrer & David Daniel Ebert

Examples

# Example 1: Use metagen object, do not estimate d
suppressPackageStartupMessages(library(meta))
data("ThirdWave")
meta1 = metagen(TE,seTE, studlab=ThirdWave$Author, data=ThirdWave)
pcurve(meta1)
#>    
#> P-curve analysis 
#>  ----------------------- 
#> - Total number of provided studies: k = 18 
#> - Total number of p<0.05 studies included into the analysis: k = 11 (61.11%) 
#> - Total number of studies with p<0.025: k = 10 (55.56%) 
#>    
#> Results 
#>  ----------------------- 
#>                     pBinomial  zFull pFull  zHalf pHalf
#> Right-skewness test     0.006 -5.943 0.000 -4.982     0
#> Flatness test           0.975  3.260 0.999  5.158     1
#> Note: p-values of 0 or 1 correspond to p<0.001 and p>0.999, respectively.   
#> Power Estimate: 84% (62.7%-94.6%)
#>    
#> Evidential value 
#>  ----------------------- 
#> - Evidential value present: yes 
#> - Evidential value absent/inadequate: no 

# Example 2: Provide Ns, calculate d estimate
N = c(105, 161, 60, 37, 141, 82, 97, 61, 200, 79, 124, 25, 166, 59, 201,  95, 166, 144)
pcurve(meta1, effect.estimation = TRUE, N = N)


#>    
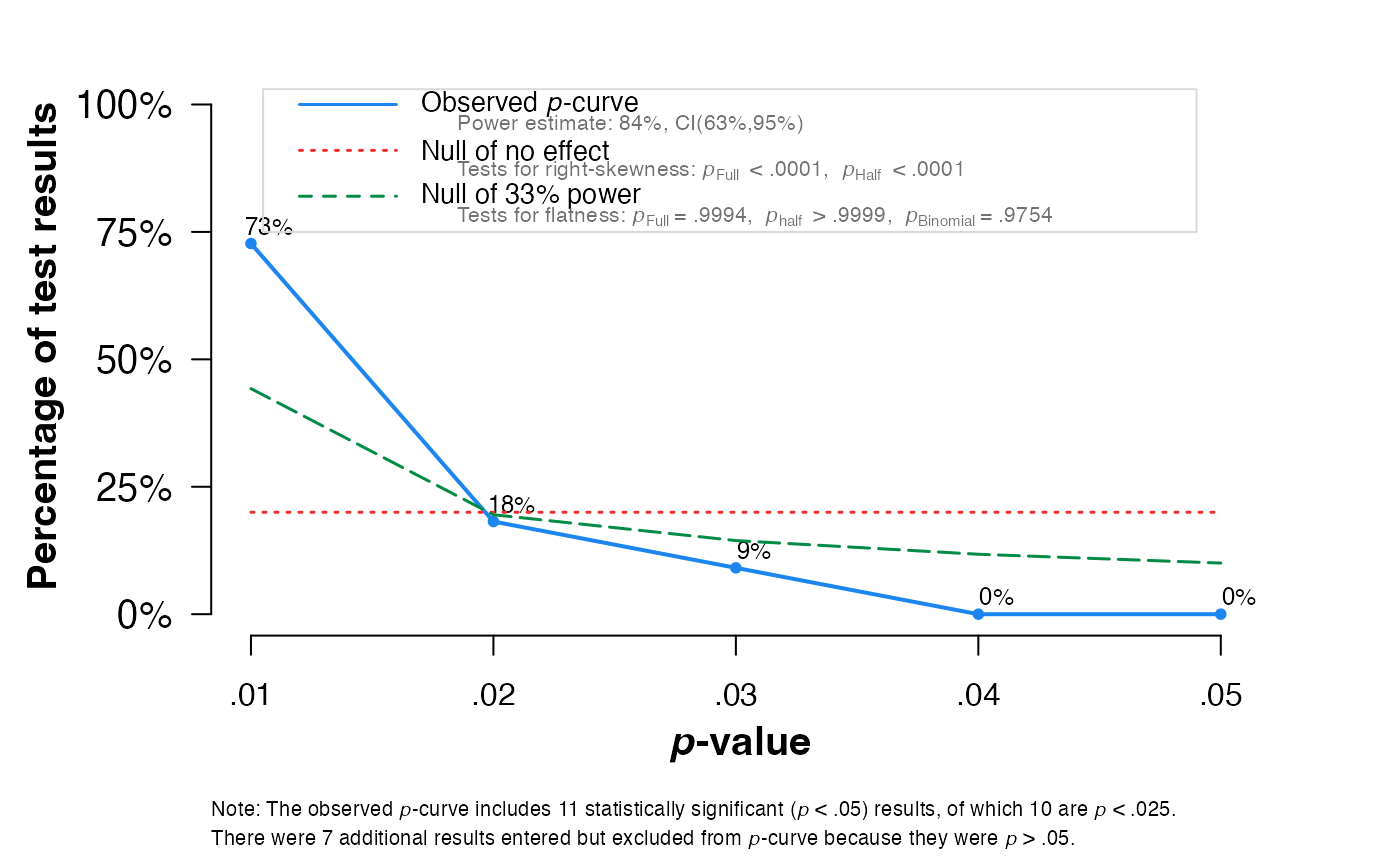
#> P-curve analysis 
#>  ----------------------- 
#> - Total number of provided studies: k = 18 
#> - Total number of p<0.05 studies included into the analysis: k = 11 (61.11%) 
#> - Total number of studies with p<0.025: k = 10 (55.56%) 
#>    
#> Results 
#>  ----------------------- 
#>                     pBinomial  zFull pFull  zHalf pHalf
#> Right-skewness test     0.006 -5.943 0.000 -4.982     0
#> Flatness test           0.975  3.260 0.999  5.158     1
#> Note: p-values of 0 or 1 correspond to p<0.001 and p>0.999, respectively.   
#> Power Estimate: 84% (62.7%-94.6%)
#>    
#> Evidential value 
#>  ----------------------- 
#> - Evidential value present: yes 
#> - Evidential value absent/inadequate: no 
#>    
#> P-curve's estimate of the true effect size: d=0.484   
#>    
#> Warning: I-squared of the meta-analysis is >= 50%, so effect size estimates are not trustworthy.

# Example 3: Use metacont object, calculate d estimate
data("amlodipine")
meta2 <- metacont(n.amlo, mean.amlo, sqrt(var.amlo),
                  n.plac, mean.plac, sqrt(var.plac),
                  data=amlodipine, studlab=study, sm="SMD")
N = amlodipine$n.amlo + amlodipine$n.plac
pcurve(meta2, effect.estimation = TRUE, N = N, dmin = 0, dmax = 1)


#>    
#> P-curve analysis 
#>  ----------------------- 
#> - Total number of provided studies: k = 8 
#> - Total number of p<0.05 studies included into the analysis: k = 4 (50%) 
#> - Total number of studies with p<0.025: k = 3 (37.5%) 
#>    
#> Results 
#>  ----------------------- 
#>                     pBinomial  zFull pFull  zHalf pHalf
#> Right-skewness test     0.312 -1.068 0.143 -1.112 0.133
#> Flatness test           0.740 -0.228 0.410  1.799 0.964
#> Note: p-values of 0 or 1 correspond to p<0.001 and p>0.999, respectively.   
#> Power Estimate: 25% (5%-79.2%)
#>    
#> Evidential value 
#>  ----------------------- 
#> - Evidential value present: no 
#> - Evidential value absent/inadequate: no 
#>    
#> P-curve's estimate of the true effect size: d=0.523   

# Example 4: Construct x object from scratch
sim = data.frame("studlab" = c(paste("Study_", 1:18, sep = "")),
                   "TE" = c(0.561, 0.296, 0.648, 0.362, 0.770, 0.214, 0.476,
                            0.459, 0.343, 0.804, 0.357, 0.476, 0.638, 0.396, 0.497,
                            0.384, 0.568, 0.415),
                   "seTE" = c(0.338, 0.297, 0.264, 0.258, 0.279, 0.347, 0.271, 0.319,
                              0.232, 0.237, 0.385, 0.398, 0.342, 0.351, 0.296, 0.325,
                              0.322, 0.225))
pcurve(sim)

#>    
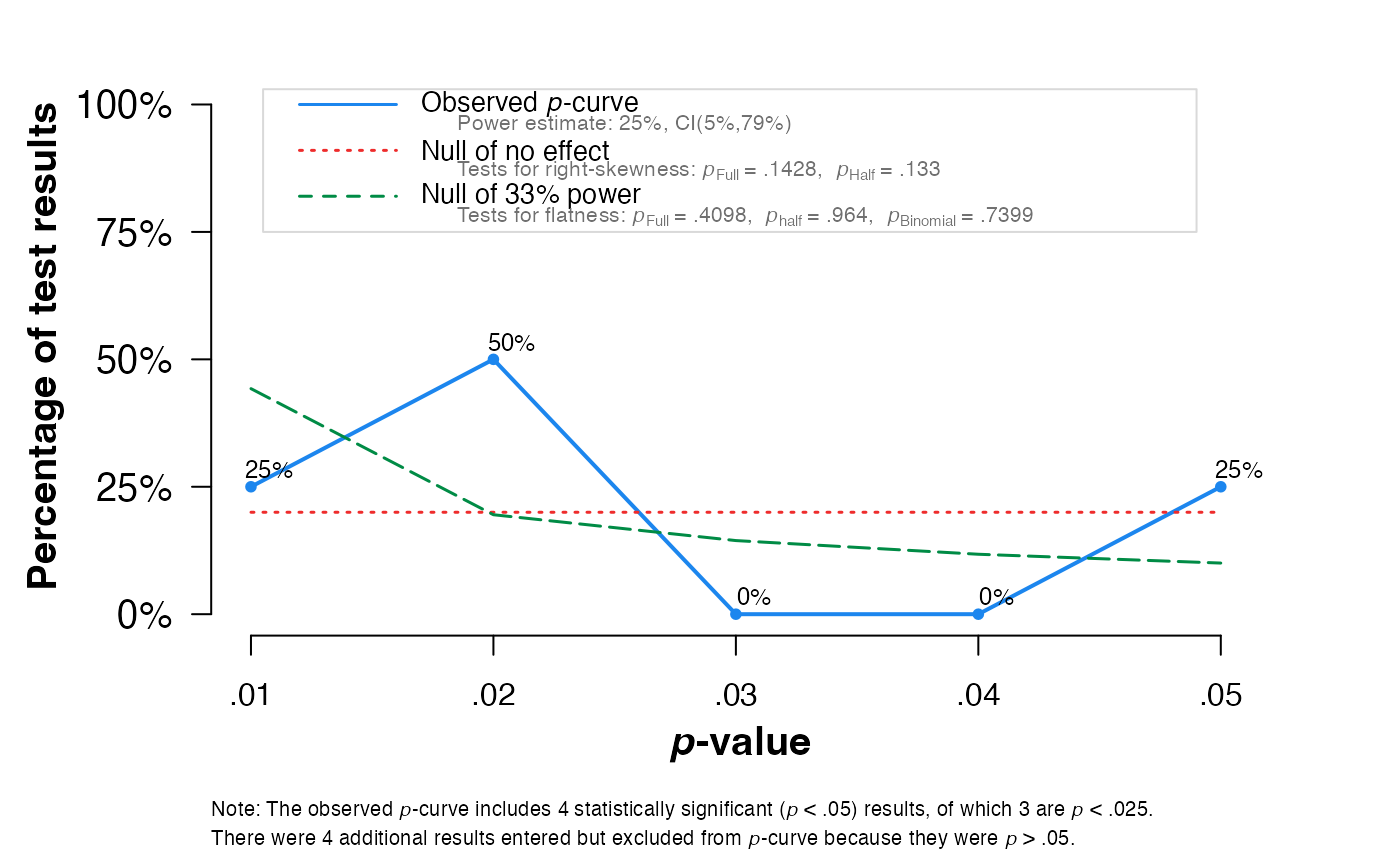
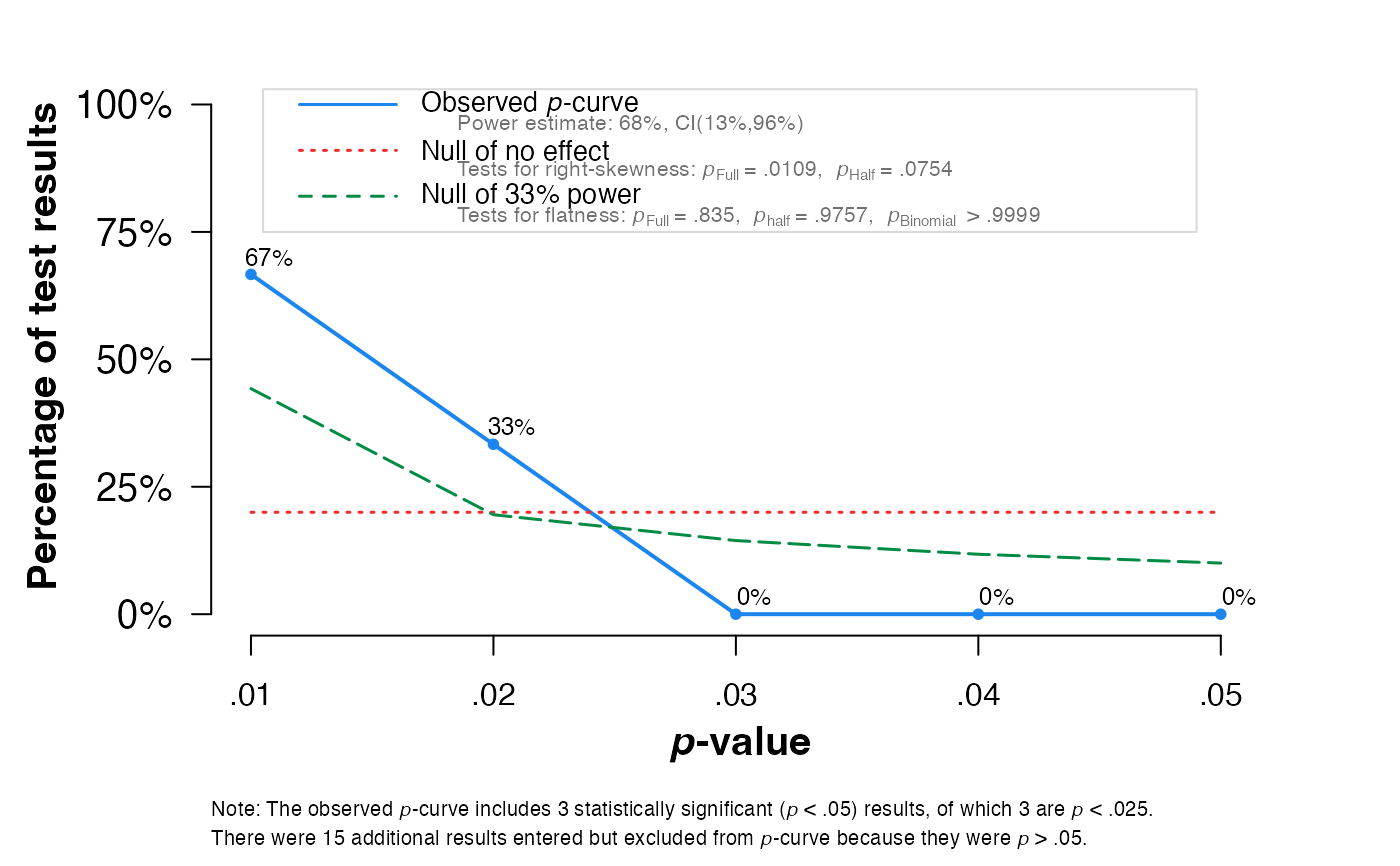#> P-curve analysis 
#>  ----------------------- 
#> - Total number of provided studies: k = 18 
#> - Total number of p<0.05 studies included into the analysis: k = 3 (16.67%) 
#> - Total number of studies with p<0.025: k = 3 (16.67%) 
#>    
#> Results 
#>  ----------------------- 
#>                     pBinomial  zFull pFull  zHalf pHalf
#> Right-skewness test     0.125 -2.295 0.011 -1.437 0.075
#> Flatness test           1.000  0.974 0.835  1.971 0.976
#> Note: p-values of 0 or 1 correspond to p<0.001 and p>0.999, respectively.   
#> Power Estimate: 68% (13%-95.5%)
#>    
#> Evidential value 
#>  ----------------------- 
#> - Evidential value present: yes 
#> - Evidential value absent/inadequate: no