Skip to contents

A priori power calculator for subgroup contrasts

power.analysis.subgroup.Rd

This function performs an a priori power estimation for a test for subgroup differences within a meta-analysis.

Usage

power.analysis.subgroup(TE1, TE2, seTE1, seTE2, sd1, sd2, var1, var2,
    two.tailed=TRUE)

Arguments

TE1

Pooled effect size (e.g., standardized mean difference, Hedges' \(g\), log-Odds Ratio or other linear continuous effect size) of the first subgroup of studies.

TE2

Pooled effect size (e.g., standardized mean difference, Hedges' \(g\), log-Odds Ratio or other linear continuous effect size) of the second subgroup of studies.

seTE1

Pooled standard error of the first subgroup of studies. Either seTE1/seTE2, sd1/sd2, or var1/var2 must be provided.

seTE2

Pooled standard error of the second subgroup of studies. Either seTE1/seTE2, sd1/sd2, or var1/var2 must be provided.

sd1

Pooled standard deviation of the first subgroup of studies. Either seTE1/seTE2, sd1/sd2, or var1/var2 must be provided.

sd2

Pooled standard deviation of the second subgroup of studies. Either seTE1/seTE2, sd1/sd2, or var1/var2 must be provided.

var1

Pooled variance of the first subgroup of studies. Either seTE1/seTE2, sd1/sd2, or var1/var2 must be provided.

var2

Pooled variance of the second subgroup of studies. Either seTE1/seTE2, sd1/sd2, or var1/var2 must be provided.

two.tailed

Logical. Should a two-tailed (TRUE) or one-tailed (FALSE) test (\(\alpha = 0.05\)) be assumed? Default is TRUE.

Value

Returns a list with five elements:

  • Power: The estimated power of the subgroup contrast, expressed as a value between 0 and 1 (i.e., 0%-100%).

  • Plot: A plot showing the effect size difference (x), power (y), estimated power (red point) and estimated power for changing effect size differences (blue line). A dashed line at 80% power is also provided as a visual threshold for sufficient power.

  • Data: A data.frame containing the data used to generate the plot in Plot.

  • Test: The type of test used for the power calculations ("one.tailed" or "two.tailed").

  • Gamma: The analyzed effect size difference calculated from the inputs.

Details

This function provides an estimate of the power \(1-\beta\) of a subgroup contrast analysis provided the assumed effect sizes in each subgroup and their dispersion measures. The function implements the formulae described by Hedges and Pigott (2001).

References

Hedges, L. V., & Pigott, T. D. (2001). The power of statistical tests in meta-analysis. Psychological methods, 6(3), 203.

See also

power.analysis

Author

Mathias Harrer & David Daniel Ebert

Examples

# Example 1: using standard error and two-tailed test
power.analysis.subgroup(TE1=0.30, TE2=0.66, seTE1=0.13, seTE2=0.14)
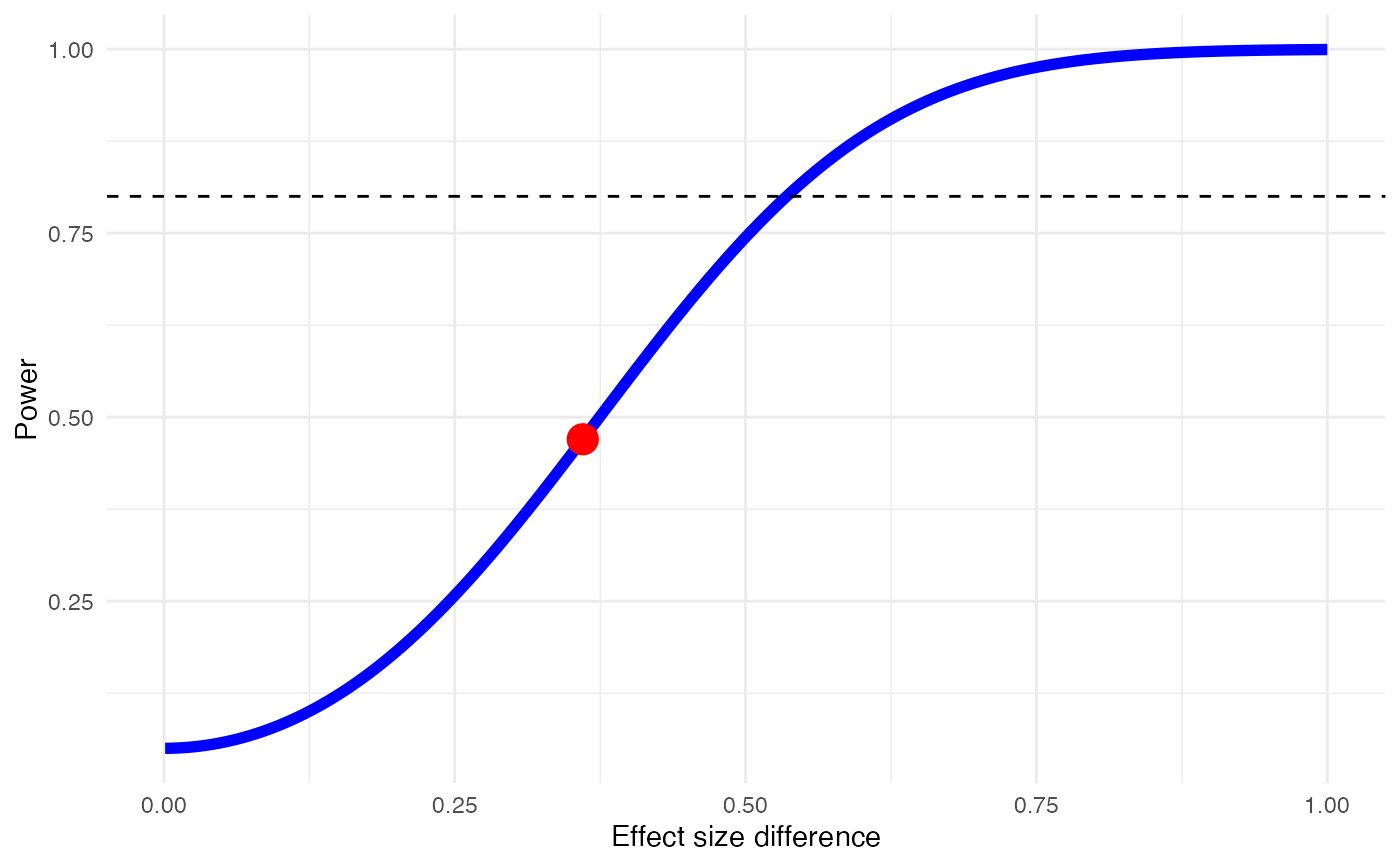
#> Minimum effect size difference needed for sufficient power: 0.536 (input: 0.36)
#> Power for subgroup difference test (two-tailed): 46.99%


# Example 2: using variance and one-tailed test
pasg = power.analysis.subgroup(TE1=-0.91, TE2=-1.22, var1 = 0.0023, var2 = 0.0078,
    two.tailed = FALSE)
summary(pasg)
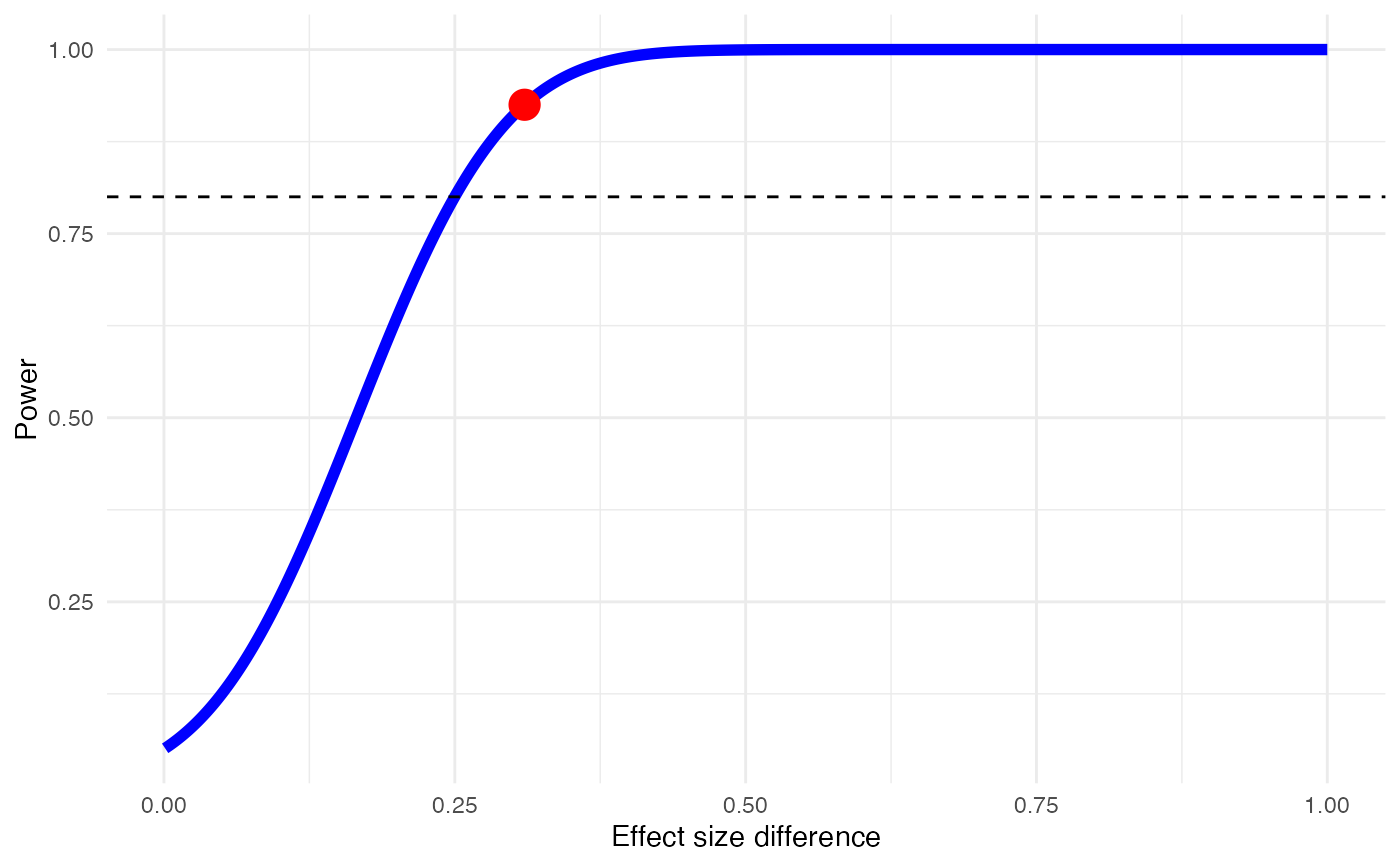
#> Minimum effect size difference needed for sufficient power: 0.25 (input: 0.31)
#> Power for subgroup difference test (one-tailed): 92.5%


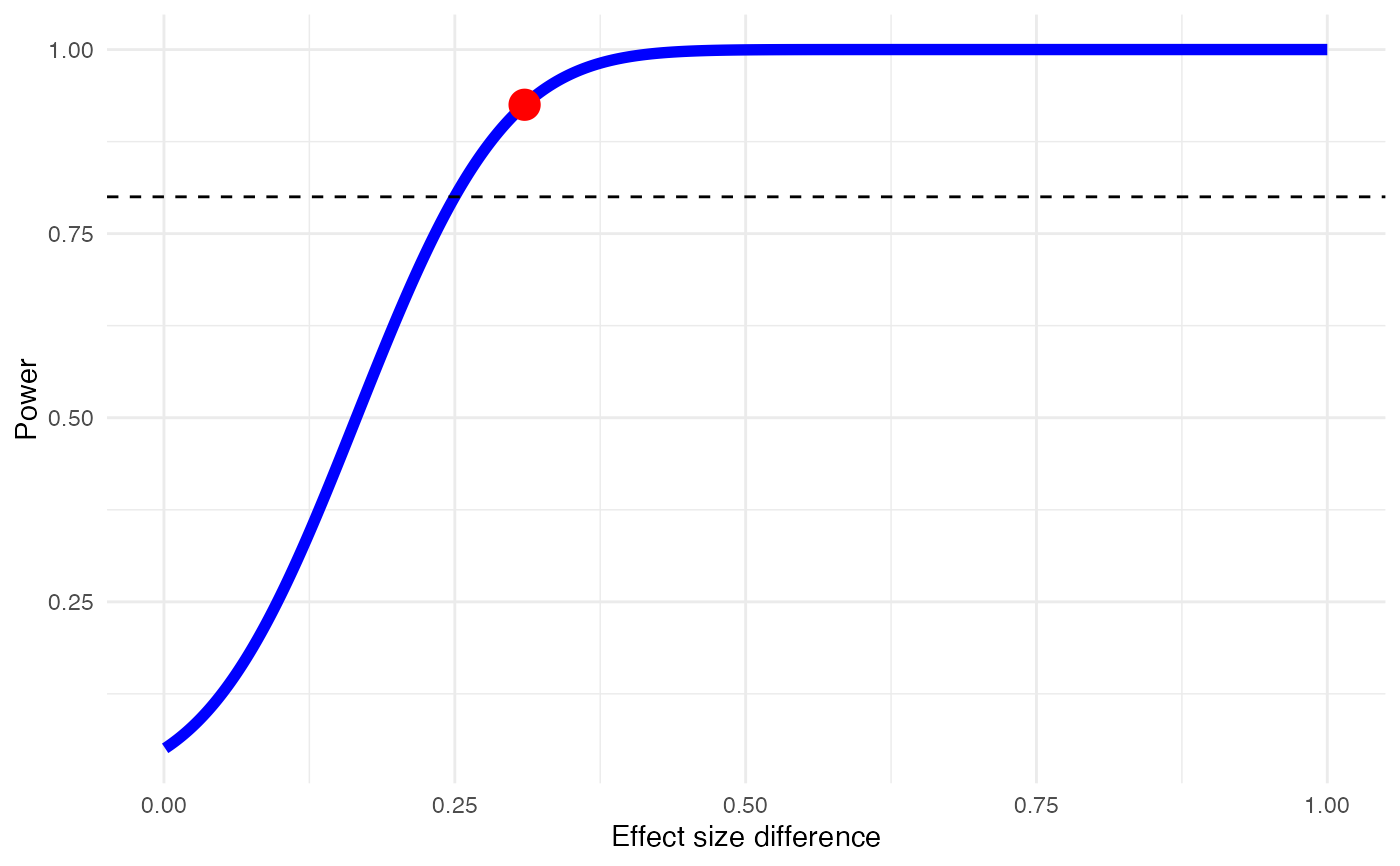# Only show plot
plot(pasg)